e continue research of the previous section
(
Mix
of backward induction and penalty term approaches I. Implementation and
results
).
We start from a function
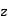 and aim to
construct
and aim to
construct
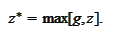
For an initial
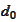 ,
form the set
,
form the set
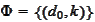 s.t.
s.t.
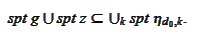
Calculate
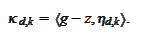
Find
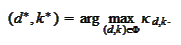
Set
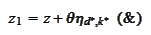 where the normalization parameter
where the normalization parameter
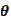 is derived from the
requirements
is derived from the
requirements
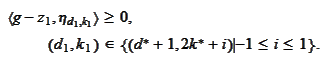 Thus
Thus
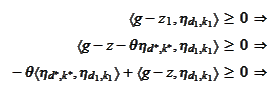
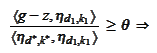
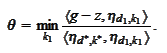
We calculate the components.
Let
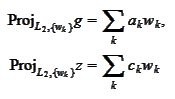 then
then
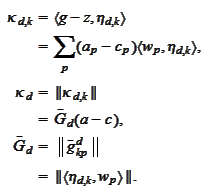 We apply the operation
We apply the operation
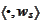 to
to
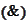 and
obtain
and
obtain
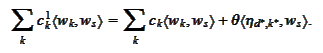 Let
Let
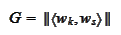 then
then
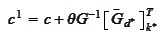 where
where
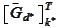 is
is
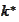 -th
row of the matrix
-th
row of the matrix
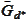 ,
transposed into a column.
,
transposed into a column.
The procedure is adapted to parallel architecture because one can subtract
several functions with non-overlapping support. Most intensive pieces of
calculation may be pre-calculated.
An adaptive extension of the procedure would involve selecting
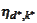 and
and
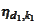 from two different classes. Indeed,
from two different classes. Indeed,
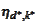 should be adapted to subtract biggest piece from the solution. The functions
should be adapted to subtract biggest piece from the solution. The functions
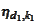 should be designed not to allow a change of sign.
should be designed not to allow a change of sign.
|