e take
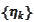to be scaled and transported hut functions. Let
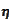be the hut
function
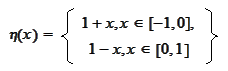and
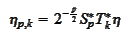for some fixed scale
.
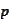One might think that selection of
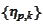should be adaptive and similar to selection of the wavelet basis
.
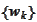We argue to the contrary that there is no reason to do such adaptive
selection. Indeed, the linear span of
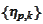includes piecewise linear functions with singularities at
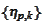's
nodes. Wavelet basis is selected adaptively mostly to compensate for lack of
smoothness of approximated solution and payoff function. A system of
transported hut functions do not have such difficulty. In fact, if edges of
the payoff function
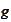are included in the set of nodes of the hut functions
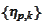then the payoff function is included in linear span of
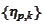exactly. We only lack precision because we approximate the solution
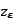with a piecewise linear functions. But for a multistep penalty function such
approximation is acceptable.
The above does not mean, however, that the scale of the probing functions may
be crude. Consider a hut function installed at the right boundary of the area
where penalty term is in effect. The right half of such hut function will
introduce a penalty value into a small area where there should not be any such
value. This consideration is the principal reason that prevents selection of
crude scale for probing functions. It also follows that the scale of the
probing functions must increase with the strength of the penalty term
(parameter
).
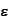To compensate, we note that we can calculate an apriori region where the
penalty function would be zero. There is no reason to place any probing
functions into such region. Such region would be time-dependent and nothing
prevents us from selecting probing functions in time-dependent manner.
|
