he adaptive techniques of the
previous chapters have one important flaw: the matrix of the problem is not
sparse. If the problem is one dimensional then it is not important. However,
as dimensionality increase, representation of solution inevitably grows in
size. The prospect of keeping a non-sparse matrix puts restrictive limits on
usefulness of the technique. We present a recipe for removing such limitation.
The recipe is not yet tested.
Consider a 2-dimensional PDE
problem
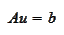solved over
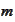point basis in every dimension. For simplicity, we do not use sparse tensor
product and evaluate it
straight:
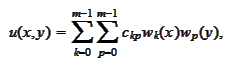
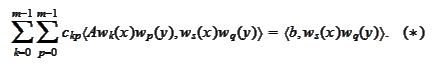We assume that the operator
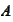admits
factorization
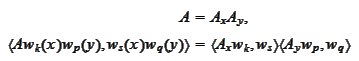thus
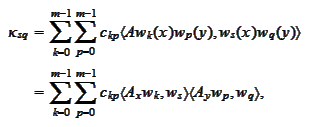
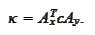We do not need to store
a
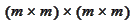matrix
.
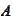Instead, we only store two
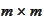matrixes
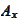and
.
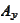We find ourselves in the situation already described in the section
(
Reduction
to system of linear algebraic equations for Black PDE
).
We change the
notation:
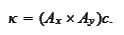It extends naturally to
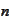-dimensional
situation. We remarked in the section
(
Reduction
to system of linear algebraic equations for Black PDE
) that the operation
"
"
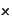commutes with matrix multiplication. It does not, however, commute with
addition. It leads to a peculiar form of matrix algebra where matrix
multiplications can be calculated but matrix additions have to be kept
preserved in form of a list.
Therefore, we cannot utilize inversion recipes of the section
(
Summary for Black
equation in case q=1
) because these would lead to very long lists.
Instead, we use preconditioners of the
form
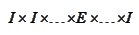where
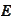are solution matrixes for one-dimensional problems, obtained from the original
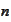-dimensional
problem via some form of projection operation.
Once preconditioning is accomplished, we get a well conditioned matrix of the
form
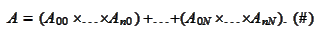That provides efficient recipe for evaluation of
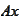for any column
.
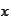Thus, GMRES is applicable.
The described above technique applies if matrix of original problem has the
property
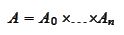or if it has a form
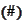to start from. The technique has wide potential because multivariate Taylor
expansion leads to the form
.
|
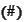