There are situations when we need the above result in form of a single matrix
that multiplies
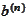 to get
to get
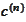 .
For example, we need it when using variational inequalities or to use it as a
partial preconditioner in a multidimensional situation. We provide a procedure
for construction of such matrix next.
.
For example, we need it when using variational inequalities or to use it as a
partial preconditioner in a multidimensional situation. We provide a procedure
for construction of such matrix next.
Due to its origins, we expect that the matrix
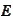 has the
property
has the
property
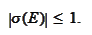 The numerical experiment in the script blackGd.py confirms it. We use this
property to remove stiffness due to finite time discretization as follows.
The numerical experiment in the script blackGd.py confirms it. We use this
property to remove stiffness due to finite time discretization as follows.
Numerical experiment in the script blackGd.py shows that with
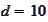 we receive a precision of final result better than precision of adaptive
wavelet approximation of the final payoff. Thus, the above summary completely
removes all problems of finite time discretization. To be precise, we get
numerical solution
value
we receive a precision of final result better than precision of adaptive
wavelet approximation of the final payoff. Thus, the above summary completely
removes all problems of finite time discretization. To be precise, we get
numerical solution
value
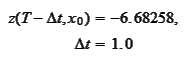 versus the
value
versus the
value
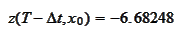 that comes from analytical solution calculated with substitution
that comes from analytical solution calculated with substitution
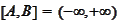 .
We use a grid consisting of 62 functions approximating the final payoff with
.
We use a grid consisting of 62 functions approximating the final payoff with
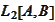 -precision
-precision
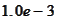 .
.
|