e apply technique of
the section (
Finite elements
) and
results of the section
(
Calculation
of approximation spaces in one dimension
) to the following problem.
According to the section (
Backward
Kolmogorov equation
), the function
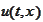is also a solution of the following problem.
Problem
(Example strong Black problem) Find
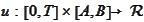s.t.
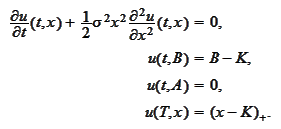
We would like to have homogeneous boundary conditions. Hence, we make a change
of the unknown
function
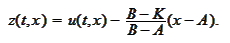We introduce the
notation
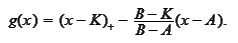
Problem
(Example strong Black problem 2)
Find
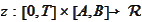s.t.
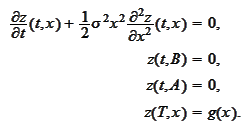
It is convenient to make a logarithmic change of variable to remove
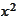from the equation. We are not going to do it. We are using this problem to
test our recipes in preparation for more elaborate problems. For example,
affine equations do not have a change of variables that would remove all
infinite terms from the PDE. The extreme stiffness that the
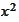multiplier brings into the problem is a persistent difficulty when solving
financial problems. In the following sections we will completely remove this
difficulty while using efficient techniques of generic nature.
The advantages of log-change should be weighted against the cost of
decomposing final payoff against wavelet basis. Without the log-change, the
payoff is piecewise linear. It may be decomposed almost instantly even in
multi-dimensional situation. After log-change it becomes difficult.
|
