e study
the mean reverting equation in preparation to an experiment in stochastic
optimization. The mean reverting equation was introduced in the section
(
Mean reverting equation
). We
make all parameters constant. A quantity
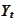 is given by an
equation
is given by an
equation
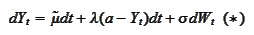 where
where
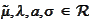 ,
,
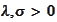 .
The
.
The
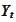 has the
meaning
has the
meaning
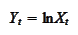 where the quantity
where the quantity
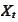 is a value of some observable market parameter that enters into a piecewise
linear payoff function. We calculate an equation for
is a value of some observable market parameter that enters into a piecewise
linear payoff function. We calculate an equation for
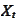 :
:
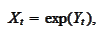
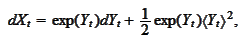
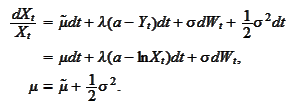
The function
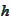 of such shape is called "butterfly" payoff. One reason for choosing such
payoff becomes apparent right away.
of such shape is called "butterfly" payoff. One reason for choosing such
payoff becomes apparent right away.
According to the section (
Backward
Kolmogorov equation
), the function
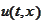 is also a solution of the following problem.
is also a solution of the following problem.
Problem
(Strong mean reverting problem) Find
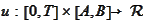 s.t.
s.t.
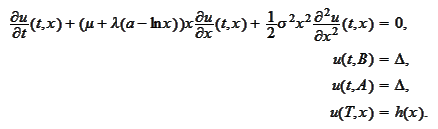
We transform to a problem with homogeneous boundary conditions. Let
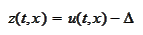 and
and
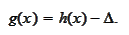
Problem
(Strong mean reverting problem 2)
Find
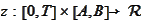 s.t.
s.t.
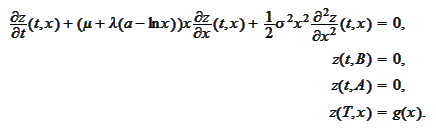
|