onsider the
equation (
Evolution with penalty
term
) involving explicit time discretization of first
order:
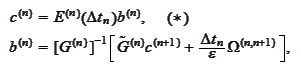
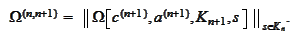 The explicit formulation is selected for calculational convenience. At the
initial time step
The explicit formulation is selected for calculational convenience. At the
initial time step
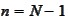 ,
the column
,
the column
 satisfies the condition
satisfies the condition
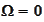 .
After evolution for one step, it falls into
.
After evolution for one step, it falls into
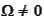 .
Under explicit formulation, it takes at least another time step for the
penalty term to take affect and the solution
.
Under explicit formulation, it takes at least another time step for the
penalty term to take affect and the solution
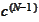 already deviated from
already deviated from
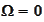 .
Clearly, we would have to make very small time steps to keep the deviation
small. Furthermore, we will pick up discrepancy on every step and accumulate
it.
.
Clearly, we would have to make very small time steps to keep the deviation
small. Furthermore, we will pick up discrepancy on every step and accumulate
it.
Therefore, we arrive to implicit
formulation:
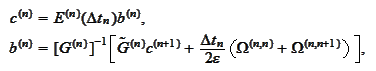
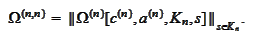 The
The
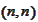 and
and
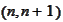 superscripts over
superscripts over
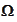 term
mark discrepancy of grids. The
term
mark discrepancy of grids. The
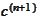 is constructed with respect to an adaptive basis selection
is constructed with respect to an adaptive basis selection
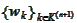 :
:
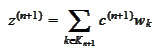 and
and
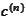 ,
,
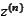 are connected similarly via
are connected similarly via
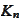 .
The
transformation
.
The
transformation
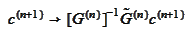 adapts
adapts
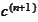 to the grid
to the grid
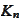 .
Hence, before performing the operation
.
Hence, before performing the operation
 ,
we apply such transformation and remove grid-dependent details from
consideration:
,
we apply such transformation and remove grid-dependent details from
consideration:
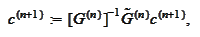
|
|
(Same grid reduction)
|
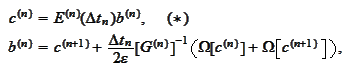
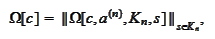
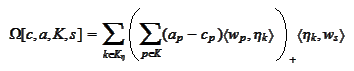 where
where
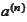 is calculated by projecting final payoff on
is calculated by projecting final payoff on
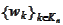 :
:
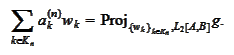
To see that such transformation is correct, put
 .
.
|