otivation and notation of this section is based on the section
(
QMF section
).
Proposition
(Biorthogonal QMF property 2) Let
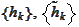 are QMF pair,
are QMF pair,
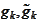 are from the definition (
Dual wavelets
) then
are from the definition (
Dual wavelets
) then
(a)
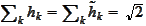 ,
,
(b)
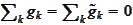 ,
,
(d)
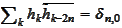 ,
,
(e)
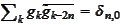 ,
,
(f)
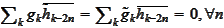 ,
,
(g)
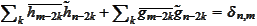 .
.
Proof
The proof is similar to the proof of the proposition
(
QMF property 2
).
|