Proposition
(QMF property 2) Let
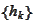 is QMF and
is QMF and
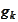 defined by the formula (
Definition of g_k
)
then
defined by the formula (
Definition of g_k
)
then
(a)
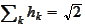 ,
,
(b)
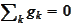 ,
,
(c)
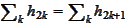 ,
,
(d)
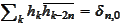 ,
,
(e)
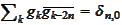 ,
,
(f)
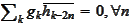 ,
,
(g)
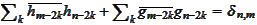 .
.
Proof
We will be using results of the section
(
Fourier analysis in
Hilbert space
) and the properties of scale and transport from the section
(
Elementary
definitions of wavelet analysis
) without further notice.
We prove
(a):
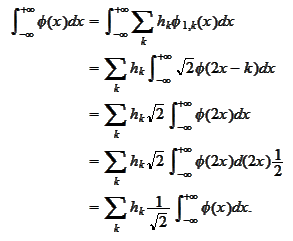
We prove (b) with the same calculation as
(a):
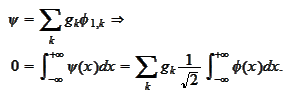
We prove
(c):
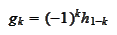 hence
hence
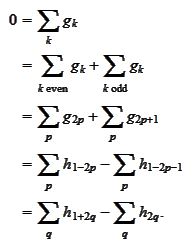
To prove (d) we
calculate
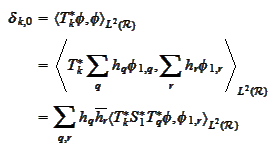
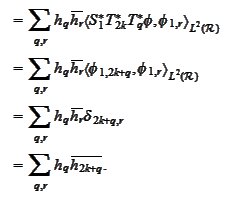 The cases (e) and (f) are similar to (d). (g) is a collection of previous
statements.
The cases (e) and (f) are similar to (d). (g) is a collection of previous
statements.
|