There following are (at least) two ways one can arrive to the equation
(
Recursive equation
) starting from the
equation (
Linear equation
).
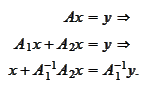
Proof
We
calculate
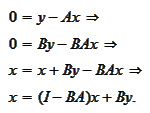
For both propositions (
Reduction scheme 1
)
and (
Reduction scheme 2
) we want to almost
invert the matrix of the original problem (
Linear
equation
). The same is true for the preconditioner
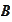 of the section (
Preconditioning
). It
appears that preconditioner
of the section (
Preconditioning
). It
appears that preconditioner
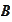 the section (
Preconditioning
) may be
used as a matrix
the section (
Preconditioning
) may be
used as a matrix
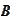 of the proposition (
Reduction scheme 2
),
provided that the
condition
of the proposition (
Reduction scheme 2
),
provided that the
condition
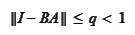 holds. The reverse statement is also true. However, the preconditioned
conjugate gradient technique converges faster as the following proposition
shows.
holds. The reverse statement is also true. However, the preconditioned
conjugate gradient technique converges faster as the following proposition
shows.
|