uppose the vector-valued random
variable
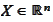 is transformed by the analytical function
is transformed by the analytical function
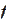 into a vector-valued variable
into a vector-valued variable
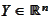 :
:
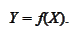 The variable
The variable
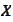 belongs to a certain class of random variables
belongs to a certain class of random variables
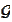 (such as the class of normal variables). We would like to evaluate statistics
of
(such as the class of normal variables). We would like to evaluate statistics
of
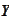 such mean and covariance matrix in some efficient way. Consequently, we select
a variable
such mean and covariance matrix in some efficient way. Consequently, we select
a variable
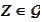 with the same statistics and use it in place of
with the same statistics and use it in place of
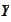 .
Since such replacement is an approximate, it is acceptable to seek approximate
procedure for evaluation of statistics of
.
Since such replacement is an approximate, it is acceptable to seek approximate
procedure for evaluation of statistics of
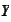 .
.
We restrict our attention to the class
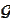 of normal vector-valued random variables. For this reason we evaluate the mean
and covariance matrix of
of normal vector-valued random variables. For this reason we evaluate the mean
and covariance matrix of
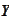 .
Let
.
Let
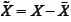 .
We treat the
.
We treat the
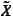 as a small quantity. We propose to approximate the mean
as a small quantity. We propose to approximate the mean
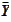 with the
sum
with the
sum
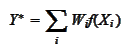 where the
where the
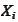 are some deterministic vectors in the value space of
are some deterministic vectors in the value space of
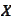 ,
,
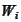 are some real numbers and the range of the index
are some real numbers and the range of the index
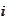 is to be determined later. We seek
is to be determined later. We seek
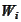 ,
,
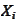 such that
such that
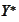 would approximate
would approximate
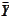 with the second
order:
with the second
order:
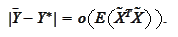
Consistently, we will be seeking approximation of the covariance matrix
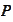
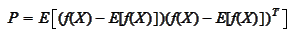 of the random variable
of the random variable
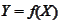 with the
expression
with the
expression
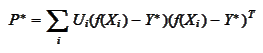 for some coefficients
for some coefficients
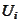 sought to
deliver
sought to
deliver
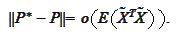
We now derive the
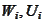 and
and
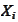 that deliver the second order approximations.
that deliver the second order approximations.
|