e are considering equations of the
form
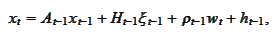
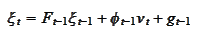where
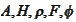are known time dependent deterministic matrixes,
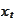is observable at time
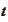random quantity,
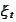is a non observable random quantity that realized (determined) itself at
,
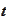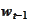and
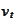are vectors of iid standard normal variables, realized at time
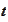and
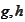are known deterministic vectors. We will say that
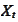is the the observable part of the information and the
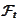is the total description at time
.
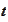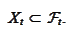
We start at time
.
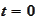We are given the distribution
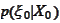and
.
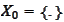We assume that the distribution for the
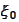is normal:
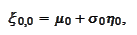where the
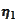is a vector of
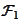-measurable
iid standard normal variables.
We will be repeatedly using the following result (see
(
Linear transformation
of random variables
)).
The summary of the procedure is as follows. We have the distribution
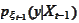from previous steps and
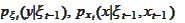from
the model. We calculate
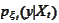through steps
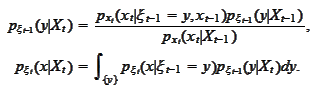The
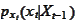is the normalization term. We do not need to calculate it explicitly. The
distributions
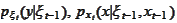come from the model.
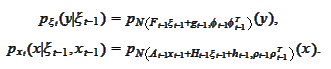The integral is calculated using the result of the previous
section:
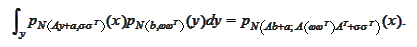
We have
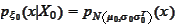for
.
We calculate
with precision up to a multiplicative normalization
constant:
We would like to put
to the
form
for some symmetrical
.
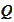We are interested only in the knowledge of
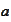and
.
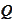Hence,
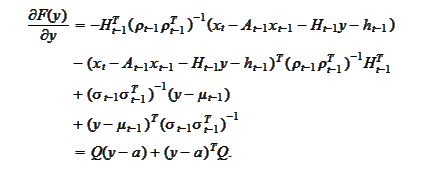
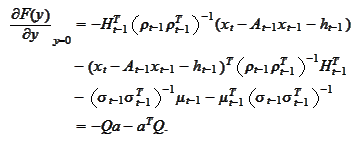
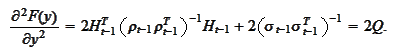Therefore,
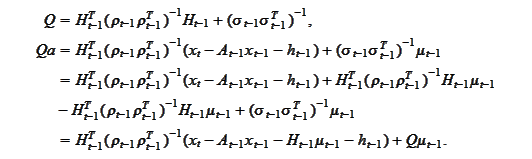
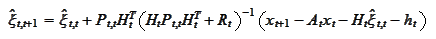The
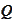is the inverse of the result's covariance matrix. We calculate it as follows
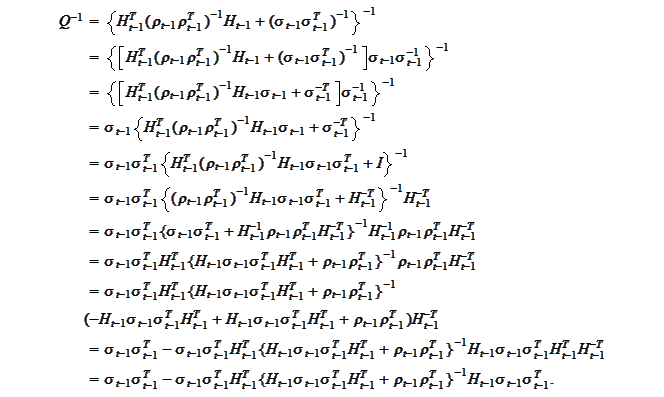Using one of the forms for
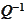above we calculate
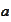as
follows
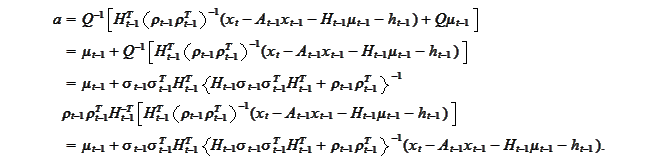We
conclude
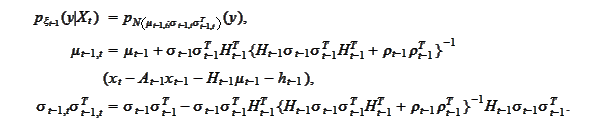
Following the outlined procedure we now
calculate
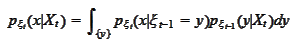where the
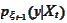we have just obtained and the
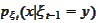comes from the
model
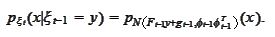Hence, we apply the formula for the convolution of normal
distributions
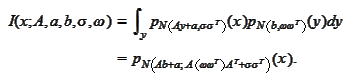We
have
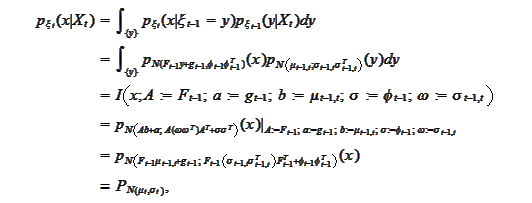
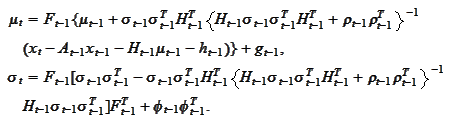The recursion is completed.
|
