We multiply the equation
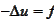 with a smooth function
with a smooth function
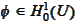 ,
integrate over the domain
,
integrate over the domain
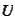 and apply the proposition (
Green formula
). We
arrive to the following weak formulation (see the section
(
Elliptic PDE section
) for review of
general theory):
and apply the proposition (
Green formula
). We
arrive to the following weak formulation (see the section
(
Elliptic PDE section
) for review of
general theory):
Problem
(Poisson equation weak
formulation 1) Find the function
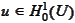 such
that
such
that
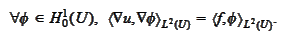
We introduce the notation
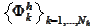 for some basis of
for some basis of
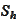 for every
for every
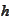 .
.
Problem
(Galerkin approximation 1) We define the
finite dimensional approximation to the solution of the problem
(
Poisson equation weak
formulation 1
) as the solution
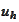 of the
problem
of the
problem
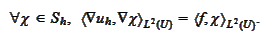
Definition
(Elliptic Ritz projection) We define the
projection
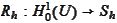 according to the
rule
according to the
rule
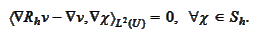
Proposition
Ritz projection has the following
property:
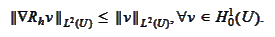
|