he concept of almost sure convergence was defined by the formula
(
Almost sure convergence
).
Equivalently, we characterize the set
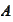 where the random variables
where the random variables
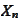 converges to the random variable
converges to the random variable
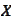 by the
relationship
by the
relationship
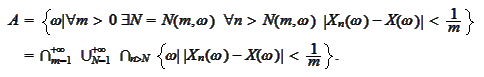
|
|
(Almost sure convergence 2)
|
The key difference from the almost sure convergence is the
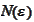 independence from
independence from
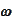 .
.
We use the
notations
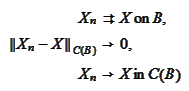 for uniform convergence. Using the technique of the section
(
Operations on sets and
logical statements
) we state that the set
for uniform convergence. Using the technique of the section
(
Operations on sets and
logical statements
) we state that the set
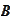 satisfies
satisfies
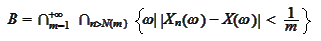
|
|
(Uniform convergence)
|
for some function
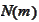 .
.
Uniform convergence implies the convergence a.s. The inverse relationship is
given by the following Egorov's theorem.
To prove the Egorov's theorem we need the continuity property of the
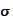 -additive
measure. It serves as a bridge between the convergence concepts defined in
terms of set algebra and the topology introduced by the probability measure.
-additive
measure. It serves as a bridge between the convergence concepts defined in
terms of set algebra and the topology introduced by the probability measure.
We now proceed with the prove of the Egorov's theorem.
|