hat happens if one takes Fourier series
of non-periodic function? To put the question in exact terms, suppose the
function
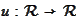 is such that the restriction of it to the interval
is such that the restriction of it to the interval
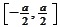 belongs to
belongs to
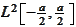 .
We form the
function
.
We form the
function
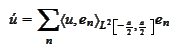 with the functions
with the functions
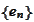 being the Fourier exponentials normalized to
being the Fourier exponentials normalized to
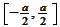 .
Such function will be the
.
Such function will be the
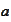 -periodic
repetition of the restriction
-periodic
repetition of the restriction
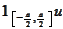 to the intervals
to the intervals
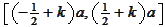 ,
,
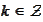 :
:
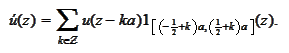
This is so because the function
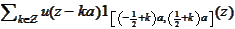 is
is
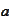 -periodic
and the sum
-periodic
and the sum
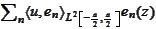 is the Fourier series of
is the Fourier series of
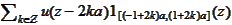 .
Then by uniqueness of Fourier series for
.
Then by uniqueness of Fourier series for
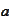 -periodic
functions we must
have
-periodic
functions we must
have
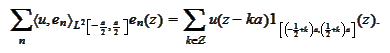
|