his is a short summary of
the technique presented in
[Longstaff]
.
We would like to calculate the
quantity
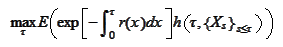 where
where
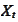 is a stochastic process in
is a stochastic process in
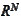 holding all the state variables, the
holding all the state variables, the
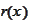 is some deterministic function representing the interest rate term structure,
is some deterministic function representing the interest rate term structure,
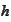 is the known payoff function depending on the path
is the known payoff function depending on the path
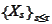 up to the moment of exercise
up to the moment of exercise
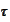 .
The functional dependence of the moment of exercise
.
The functional dependence of the moment of exercise
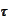 on the state variables
on the state variables
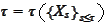 is the subject of optimization.
is the subject of optimization.
Suppose the
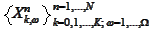 is the result of Monte-Carlo simulation of the stochastic process
is the result of Monte-Carlo simulation of the stochastic process
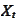 with
with
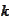 being the time index,
being the time index,
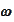 being the simulation index and
being the simulation index and
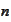 being the dimension index,
being the dimension index,
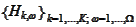 is the result of immediate exercise
is the result of immediate exercise
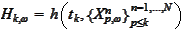 ,
,
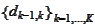 is the discount factor between neighbor indexes
is the discount factor between neighbor indexes
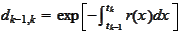 .
.
Introduce an array
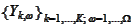 and a set of functions
and a set of functions
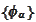 acting
acting
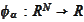 .
.
Start with
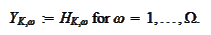
For
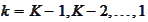 do the
following:
do the
following:
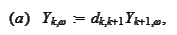
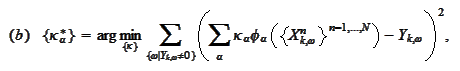
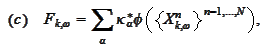
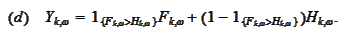 The answer is
The answer is
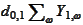 .
We do not proceed to step k=0 because the cross sectional information
.
We do not proceed to step k=0 because the cross sectional information
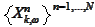 collapses to a point at this step. The obtained this way value is biased high
because this is a forward looking procedure. If we continue the MC simulation
on the obtained strategy
collapses to a point at this step. The obtained this way value is biased high
because this is a forward looking procedure. If we continue the MC simulation
on the obtained strategy
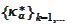 then we get a biased low value because the strategy is suboptimal.
then we get a biased low value because the strategy is suboptimal.
The motivation for the steps above is the following. The
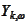 is the value of the quantity in question at time
is the value of the quantity in question at time
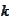 given the information
given the information
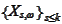 . Hence, the starting condition is obvious. The sum
. Hence, the starting condition is obvious. The sum
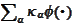 is used to construct the function that depends only on available information
and best approximates the Y. Hence, we discount the Y from the previous step
with (a), find the best approximation in (b), chose the best strategy and
calculate the new Y in (c) and (d).
is used to construct the function that depends only on available information
and best approximates the Y. Hence, we discount the Y from the previous step
with (a), find the best approximation in (b), chose the best strategy and
calculate the new Y in (c) and (d).
The step (b) may be performed using the Normal Equations technique presented
in the next section.
The step (b) is unstable if the time step is small and
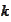 is close to the origin. In such situation the
is close to the origin. In such situation the
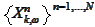 does not contain much
cross-
does not contain much
cross-
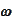 information because all the
information because all the
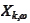 originate from a single point
originate from a single point
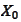 and did not have time to evolve. For this reason the procedure is not
effective if the exercise is immediately possible.
and did not have time to evolve. For this reason the procedure is not
effective if the exercise is immediately possible.
|