he closeness of normal variables with
respect to the linear transformation may be traced to the Central Limit
theorem that we introduce in the present section.
Better versions of CLT are presented in the section
(
Central limit theorem (CLT)
II
).
To see why CLT is true, consider the following calculation.
Suppose the iid variables
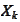 have the common density
have the common density
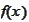 .
We calculate the Fourier transform (=characteristic
function)
.
We calculate the Fourier transform (=characteristic
function)
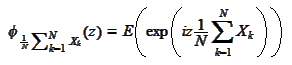
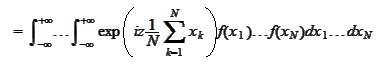 We use independence of
We use independence of
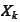 .
.
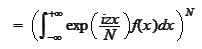 We expand the
We expand the
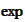 in powers of
in powers of
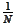 .
.
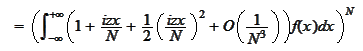 We use
We use
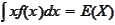 ,
,
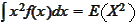 ,...
,...
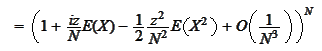 We apply the transformation
We apply the transformation
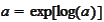 .
.
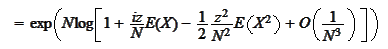 We utilize
We utilize
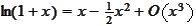 ,
,
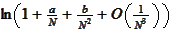 =
=
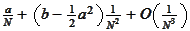 ,
,
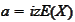 ,
,
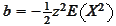 .
.
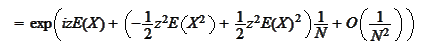
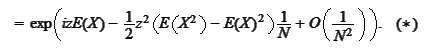 For a normal distribution
For a normal distribution
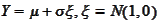 we
calculate
we
calculate
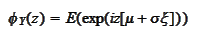
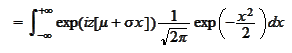
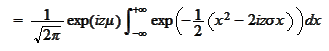
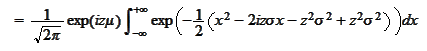
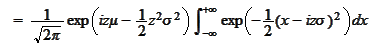 We use
We use
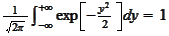 .
.
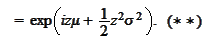 The Fourier transform is an isometry in
The Fourier transform is an isometry in
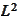 .
By comparing (*) with (**) we conclude
.
By comparing (*) with (**) we conclude
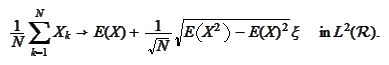 It still remains to derive the pointwise convergence. We postpone such issues
until the section (
Vague
convergence
). Advanced versions of CLT are presented in the section
(
Central limit theorem (CLT)
II
).
It still remains to derive the pointwise convergence. We postpone such issues
until the section (
Vague
convergence
). Advanced versions of CLT are presented in the section
(
Central limit theorem (CLT)
II
).
|